数学良問集もくじ＞§01 まずはここから＞答え


ひとめでわかるように、答えのページは背景が白いのよ。


　　　セクション1「まずはここから」の答え　　



Q01-01 有名できれいな問題
【コメント】
空色じゃなくてオレンジじゃんって思った人には、私は「その空は「夕やけ」かもしれません…」と言ってしまいます。
でも、名曲です。

というわけで、PCの画面で膨大な計算式を見るのは大変なので大幅にCUTしました。
ホンネは、図をかくのが面倒くさいからかもしれませんけど、大きな声じゃ言えません…。
そのかわり、いろいろな言葉を使わせていただきましたが、結果的に、やっぱりわかりにくい…(泣)
でも、答えのページは、すべて「実際に解いてくださった人」へ向けて書いているので、このくらいでOKですよね。

【雑解】
とりあえず：ヒント図（「ねこ？」）の緑の線分の交点をEとする。
ファーストステップ：すると△EBCは正三角形なので、扇型EBCの面積もわかるため、栗型EBCの面積がわかる。
セカンドステップ：(四分円ABC)−(栗型)を計算すると、朝顔のつぼみ型ABEの面積となる。
ラストステップ：ここで、図をよく見ると(求めたい面積)＝(正方形ABCD)−(朝顔のつぼみ型)×4だとわかる。
(↑実はこのラストステップの式はspecial thenksのakanedotさんに教えていただきました。スマートですね。)
答えはたぶん、(π/3＋1＋√3)r2だと思います。
(追記：そんなわけないですね…。(π/3＋1＋√3)a2です！
　　　つちのこさん、ご指摘ありがとうございます！)
(追追記：はい、正方形より大きくなるわけありませんよね(笑)
　　　もうボロボロです…(恥)
　　　(π/3＋1−√3)a2が正解です！
　　　私の写しミスです…。つちのこさん、akanedotさん、本当にありがとうございました！

最も標準的な解き方を書いたつもりですが、たくさん別解があります。
いつか、書いてみたいですね。

←問題へ戻る
ディクからの暗号●





Q01-02 きれいな問題
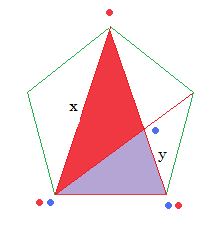
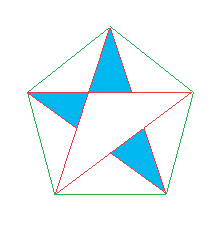
【コメント】
♪流星がこぼれた〜、も名曲だと思います。
イントロが好きです。

中学生でも解けるということですが、なかなか面倒くさい。
ここでも同じく、計算式はだいぶ省略。

【雑解】
正五角形の1つの内角が108°であることを思い出すと様々な部分の角度がすぐにわかる。
よって、△赤と△青（なんと、重なった部分は紫にするという芸の細かさ(笑)）は二等辺三角形でかつ相似。（中二の範囲）

対角線の長さをx、△青の底辺をyとすると、相似より、
x：2a＝2a：y, 2a＋y＝x
がわかる。
解の公式を使わず平方完成を使えば中三の範囲で、x＝(√5＋1)a がわかる。
同様に、y＝(√5−1)a

あとは簡単で、
二等辺三角形は底辺ともう一辺がわかれば三平方の定理（中三の範囲）で高さがわかるので、
(正五角形の面積)＝(二等辺三角形2a,2a,x)×2＋(二等辺三角形x,x,2a)
↑こんな書き方はたぶんないけど、わかるよね。
これを計算すると、確か、
{(√5＋1)√{(5−√5)/2}＋√(5＋2√5)}a2……(答)

…きたない。

akanedotさんは、
{(3＋√5)(√(5＋√5)/2)＋(1＋√5)(√(5−√5)/2)}a2/2
と教えてくださいました。同じらしいです。ホントに？
私の答えの方が式が少ないですが、こっちのほうがキレイね…(汗)

（2）の星の面積はどう解いてもいいのですが、右のように考えると二等辺三角形が2種類しか出ないので比較的ラクかな、と私は考えてますが、答えは作成中…。
akanedotさん、解いてくれませんか〜(笑)

…と嘆いていたら、解いてくれました(笑)
答えは、
{(√5−7)√((5＋√5)/2)＋(√5＋11)√((5−√5)/2)}a2/2
とのことですが、なんと、(正五角形)−(5つの三角形)と解いたそうです。
やっぱりその方が速いんですかね？
私もなんだかやる気になってきました！

ここからは03/29/2008の追記…
というわけで、どこまでキレイにできるか、もう一度、私、やってみました！
もちろん、すべて手計算です！

正五角形の面積：(√(25＋10√5))a2

星形の面積：(5−√5)3/2a2/√2

これでいかがかしら？

と、何回追記しているのかわかりませんが、冷静に考えたら正五角形の面積は、5a2tan54°ですね。
これと上の結果からtan54°の値がわかるとみなせばほんのちょっと有益かもしれませんね。

←問題へ戻る

 わかりやすい図その1

わかりやすい図その2
ディクからの暗号●





Q01-03 因数分解（(3)は(2)をもとにした手作り問題）
【コメント】
ずっと口ずさんでいたくなりませんか、「テレコ」って。
…なりませんね。

いずれもいい問題でしたが、解けましたか？
そういえば、「こうべき」を変換しても「降べき」って出ません！なんとかしてよ、ビルゲ＊ツさん！
【解答】

(1) x4＋4

＝x4＋4＋4x2−4x2　　←ヒントに従って

＝(x2＋2)2−(2x)2　　←平方完成＆次につながる変形

＝(x2＋2x＋2)(x2−2x＋2)　　←2乗の差の公式＆降べきの順に整理＆答

もし、虚数の範囲まで展開すると、

＝(x＋i＋1)(x＋i−1)(x−i＋1)(x−i−1)

これはこれでキレイですが。

←問題へ戻る

 【解答】

(2) (a2−1) (b2−1)−4ab

＝(ab)2−a2−b2＋1−4ab　　←とりあえず展開

＝(ab)2−(a＋b)2−2ab＋1　　←point：a＋bとabで表してみた

ここで「見えれば」解けちゃいますが、見えましたか？

＝(ab)2−2ab＋1−(a＋b)2　　←並べ替えただけ＝次につながる変形

＝(ab−1)2−(a＋b)2　　←前の方を平方完成

＝(ab＋a＋b−1)(ab−a−b−1) ←答

やや不思議ですが（3）も同様にして解ける。

(ab＋a−b＋1)(ab−a＋b＋1)……(答)

←問題へ戻る
ディクからの暗号 ●





Q01-04 あみだくじ(手作り問題)
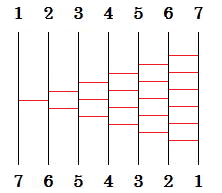
【コメント】
「にゅい〜んとした線」て何ですかね。

【解答】
右図のとおり！

もちろん答えはいくつもありますがこれが一番キレイでしょ？
横線は21本ですがこれが最小の本数。
実は、たてがn本の場合もこんな感じで表せる。

←問題へ戻る

 これが答え！
ディクからの暗号●





Q01-05 大小関係（(1)と(2)は手作り問題、(3)は筑波大改）
【コメント】
そういえば、問題のタイトルがつまらないですね…。

【解答】（1）
(※面倒くさいから、1.1の1.1乗根を｛1.1｝のように書くことにさせてもらいま−す！)

暗算でどこまでいけるのでしょうか！
まず、｛1.1｝と｛2.2｝を見て、両方を2.2乗する。
すると暗算で｛1.1｝2.2＝1.21、｛2.2｝2.2＝2.2がわかり、
｛1.1｝＜｛2.2｝が判明。
あとは、こんな感じのことを繰り返すのですが、｛2.2｝と｛4.4｝、｛3.3｝と｛6.6｝などのようにうまく二組を選んで大小比較する。
暗算では｛5.5｝で少々悩みますが｛5｝と｛2｝では｛5｝の方が小さいから｛5.5｝と｛2.2｝でも｛5.5｝の方が小さいのでは、とちょっと適当にすませます…。
最終候補はやはり｛2.2｝と｛3.3｝になります。
先に方法を言うと、この二つを6.6乗すればいいのですが、かなりの僅差なので、ここでは泣く泣く紙とペンを使います。
2.23＝10.648、3.32＝10.89より、最大値は｛3.3｝です。

また、形を見るとすべてxのx乗根になっているから、そんなグラフを書いて検証すればいいような気もします。
すると、eのe乗根が最大になることがわかります(eは自然対数の底で2.718…という無理数)。
選択肢でいうと、やはり｛2.2｝か｛3.3｝のどちらかになりそうですね。
しかし、ここからは、極大値の左右でグラフの傾きを調べたりしなければいけなそうなので、きっと面倒くさいですから、諦めます…。

←問題へ戻る

 【コメント】
この解答欄、大変見にくいですね。
力不足で、すみません…m(_ _)m
(（3）の解答は（2）の下です)

【雑解】（2）
問題の、上の式をA×Bとおくと、下の式は
(A−1)(B＋1)
となる。
ここで、A＝B＋101ということに注意して、
(A−1)(B＋1)
を展開すると、
　AB＋A−B−1
＝AB＋(A−B)−1
＝AB＋101−1＞AB

∴下の式の方が大きい。

【雑解】（3）
logをとって、y＝(logx)/xのグラフを書いてもいいし、
両辺を1/(eπ)乗してy＝xのx乗のグラフを書いてもいい。
いずれにせよ、グラフを書かないと解けない問題ですが、書けば簡単に解けます。

結論は「eπの方が大きい」となります。

結果だけ覚えておくならば「いっぱい」なのはイーのパイ乗と覚える(？)

←問題へ戻る
ディクからの暗号●





Q01-06 あみだくじリターンズ
【コメント】
ついに「にゅい〜んとした線」解禁ですね。
でもさっきから「にゅい〜んとした線」って何なの？

細かいことは置いておいて、解答は数学的帰納法をありがたく使わさせていただきます。

【解答】
横棒の本数をnとする。
n＝1のとき
これは横棒が1本のときで、成り立つのは当たり前。
n＝kのとき成り立つとする。
n＝k＋1のとき
これは、成り立っているあみだくじに1本横棒を足しただけなのでその部分で結果が入れ替わるだけで、やはり成り立つ。
よって、nが、すなわち横棒の本数が、自然数ならいくつでも成り立つことが、数学的帰納法により証明できた。

「にゅい〜んとした線」がないものとして、解答を書いてしまいましたが、あってもこんな感じでいいですよね？

私、数学とか苦手なのでよくわかんないんですけど…。

←問題へ戻る

ディクからの暗号●