| Q14-01 | 桪偟偄婥帩偪偵側傟傞栤戣(庤嶌傝栤戣) |
|---|---|
| 亂僐儊儞僩亃 巹偼偙偺幃傪尒偮偗偨偲偒偵偲偰傕姶摦偟傑偟偨丅 朸n僠儍儞僱儖偺6n帪娫僥儗價偺25nkm儅儔僜儞偺僑乕儖傛傝傕姶摦丅 亂夝摎亃 a偲b偺嵟戝岞栺悢傪k偲偡傞偲丄a亖a'k,b亖b'k(a'偲b'偼屳偄偵慺)偲偍偗偰丄傕偪傠傫g亖k偱偁傞丅 a'偲b'偑屳偄偵慺側偺偱丄l(僄儖)亖a'亊b'亊k偱偁傞丅 傛偭偰丄ab亖lg乧乧(摎) 桪偟偄偱偼側偔丄堈偟偄栤戣偱偟偨丅 偍屻偑傛傠偟偄傛偆偱丅 仼栤戣傊栠傞 | |
| 僨傿僋偐傜偺埫崋 | 仠 |
| Q14-02 | 偍偍偭摨偠偩 |
|---|---|
| 亂僐儊儞僩亃 乽僇僾儗僇悢乿偼傑偩斾妑揑怴偟偄傜偟偄丅 亂夝摎亃 偦傫側傢偗偱(丠)夝摎嶌惉拞乧丅 仼栤戣傊栠傞 | |
| 僨傿僋偐傜偺埫崋 | 仠 |
| Q14-03 | 偡偘乕丄搶杒戝丅(搶杒戝嶲峫) |
|---|---|
| 亂僐儊儞僩亃 偙偆偄偆偄偄擖帋栤戣偵弌夛偊偰姶摦抳偟傑偟偨乧丅 亂夝摎亃 偟偽傜偔姶摦偵怹傝偨偄偐傜傑偨崱搙乧丅(仼偍偄偭乧) 仼栤戣傊栠傞 | |
| 僨傿僋偐傜偺埫崋 | 仠 |
| Q14-04 | 5偮傕偁傞偲傕偼傗儔僢僉乕姶偼側偄 |
|---|---|
| 亂僐儊儞僩亃 幚偼丄傕偲傕偲偼乽2004擭乿偲偄偆栤戣偱偟偨丅 4擭偵堦搙偔傜偄峏怴偟傑偡乧丅 摛抦幆両 1111乧乧偺傛偆偵1偑暲傫偩惍悢偼偨偄偰偄崌惉悢(慺悢偱側偄悢)偩偲巚偄傑偟傚偆丅 慺悢側偺偼11偲丄偦偺師偼1111111111111111111(19偗偨)偱偡丅 偗偨偺悢偑嬼悢側傜偦傟偼11傪慺場悢偵帩偮偟丄 偗偨偺悢偑3偺攞悢側傜111偱妱傝愗傟偰丄偙偄偮偼3亊37偱偁傞丅 偝傜偵丄 _5偗偨亖41亊271 _7偗偨亖239亊4649 11偗偨亖21649亊513239 13偗偨亖53亊79亊26531653 17偗偨亖2071723亊5363222357 偱偁傞丅 偝傜偵丄 惣楋偑4偺攞悢偱偁傞擭偼2/29傑偱偁傞偆傞偆擭偩偗偳丄 惣楋偑100偺攞悢偱偁傞擭偼2/28傑偱偺偆傞偆擭偩偗偳丄 惣楋偑400偺攞悢偱偁傞擭偼2/29傑偱偁傞偆傞偆擭丅偙偺慜偺2000擭偑偦偆偱偟偨丅 偦傫側偙側傫丄偠傖側偐偭偨丄偦傫側偙傫側偱夝摎偵峴偒傑偟傚偆両 亂嶨夝亃 77777亖7亊41亊271偲慺場悢暘夝偱偒傞偨傔丄 怴堦榊偼7嵥丄梇嶌榊偼41嵨偱抋惗寧擔偼271擔栚偲側傞(傑偝偐271嵨偱偼側偄偩傠偆偐傜偹)丅 2008擭偼偆傞偆擭(塸岅偱leap year(捈栿偡傞偲乽挼傇擭乿))側偺偱丄9/27惗傑傟丅 惓妋偵偼丄4擭偵2搙峏怴偡傞偐傕乧丅 1搙栚偼惣楋傪曄偊偰丄2搙栚偼乽抋惗擔偑傗偭偰偔傞偲偒乿傪乽抋惗擔偑傗偭偰偒偨偲偒乿偵捈偡偙偲偱偟傚偆両 (偙偺夝摎偵偼乽壗擭惗傑傟乿偲彂偄偰傑偣傫偑丄栤戣偱栤傢傟偰偄傞偺偱杮摉偼彂偐側偄偲僶僣側偺偱偡偑丄偦傟傕偙偙偵彂偔偲丄峏怴偺偲偒傑偨擭傪1擭偢傜偟偨傝偟偰柺搢側偺偱丄偁偊偰彂偄偰傑偣傫丅偮傑傝庤敳偒偱偡乧) 傎傫偺偪傚偭偲晄巚媍側偺偼丄惣楋傪偳偺傛偆偵曄偊偰傕丄7嵥偲41嵨偼曄傢傜側偄偲偄偆偙偲偱偡偹両 仼栤戣傊栠傞 | |
| 僨傿僋偐傜偺埫崋 | 仠 |
| Q14-05 | 擖傟偨偔側偭偨悢傪擖傟偪傖偊偽偄偄偠傖側偄(峀拞攖) |
|---|---|
| 亂僐儊儞僩亃 僕儍仏巕偵偼杮柤偑掕傔傜傟偰偄傑偣傫丅(仼杮摉偱偡) 偒偭偲丄偛椉恊偺扨弮儈僗偱偟傚偆丅(仼傫側傢偗側偄) 偲偙傠偱丄忋偺栤戣偲偙偺栤戣偑"11111"偲偄偆悢帤偱寢偽傟偰偄傞傢偹丅 偙偺栤戣傕晄巚媍側崄傝丅壥偨偟偰偍枴偼偄偐偑偐側丠 亂嶨夝亃 側傫偐偆傑偄傗傝偐偨偼偁傞偺偐偲峫偊偢偵傆偮偆偵夝偔仛 傕偪傠傫丄312亄312亄312亄312亄312亄312亄312傪7丒312偲偍偔偔傜偄偺岺晇偼偡傞偗偳偦偺偔傜偄偱偁傞丅 仩亖28乧乧(摎) "11111"偲偄偆悢帤偩偗偱側偔丄"擭"偲偄偆僉乕儚乕僪偱傕寢偽傟偰偄傑偟偨丅偍枴偼嵟崅偱偡偹丅 偊偭丄29傪擖傟偨偔側傝傑偟偨偐丠 忋偺栤戣偑偆傞偆擭側偺偱偡偐傜丄偙偺栤戣偑仩亖29偩偭偨傜丄忋偺栤戣偲2擭(栤丠)楢懕偱偆傞偆擭偵側偭偰偟傑偄傑偡乧丅 仼栤戣傊栠傞 | |
| 僨傿僋偐傜偺埫崋 | 仠 |
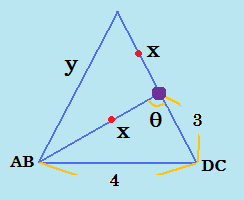
| Q14-06 | 堄奜偲柺搢偔偝偄戝偒偄媟棫偺栤戣丅 | |
|---|---|---|
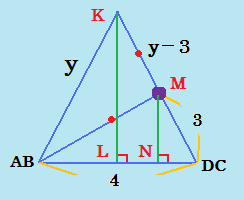
| 亂僐儊儞僩亃 恷擖傝偺慜偱偼婥傪幐偭偰偟傑偆屲榊偝傫偼丄偙傫側戝偒側媟棫偱壗傪偟偰偄偨偺偱偟傚偆偐乧丠 偙偺恖偑悢妛嬫柉側傜乧乧傕偟傗丄偙偺栤戣傪夝偄偰偄偨偺偐丠両婋側偄偐傜崀傝偰両 亂夝摎亃 屲榊偝傫偑崀傝偰偒偨偺偱摎偊傪尒偣偰傕傜偄傑偡丅 塃忋偺恾偺傛偆偵x丄y丄兤傪掕傔偰丄壓偺嶰妏宍偱丄梋尫掕棟傛傝x2亅7亅6xcos兤亖0乧嘆 忋偺嶰妏宍偱傕摨條偵偟偰丄y2亖2x2亅2x2cos(180亅兤)乧嘇 兤傪徚偟偰丄x傪媮傔傞曽恓偵丅 嘇偺cos(180亅兤)偼亅cos兤偵側偍偟偰丄嘆偺椉曈偵x2丄嘇偺椉曈偵3傪偐偗傞偲丄6x2cos兤偑徚偣偰丄x偩偗偺3師幃偵側傞丅偁偲偼揔摉偵悢帤傪擖傟偰挷傋傞偩偗偩偑偙傟偱偼柺搢偔偝偄偺偱丄 x(x(x亄3)亅25)亅27亖0偲偡傟偽妡偗嶼偺夞悢偑奿抜偵尭傞丅x佮4.3偑傢偐傞偺偱丄y佮7.3偲側傝丄僀)偑惓夝丅 幚偼丄偙偺栤戣偺嵹偭偰偄偨杮偱偼嶰暯曽偲憡帡偩偗偱夝偄偰偄偨丅 亂暿嶨夝亃 塃壓偺恾偺傛偆偵偄傠偄傠傗偭偰丄NC傪a偲偱傕偍偄偰偍偔丅嶰暯曽偺掕棟傪2夞巊偭偰丄AM2亖AN2亄MC2亅NC2 偙偺幃偲丄仮MNC偲仮KLC偑憡帡偱偁傞偙偲傛傝a偑徚偊丄y偩偗偺3師幃偵側傞丅偁偲偼忋偲摨偠傛偆偵傗偭偰丄y佮7.3偱丄傕偪傠傫丄僀)偲偄偆摨偠摎偊丅 忋偺屲榊偝傫偺夝朄偺傎偆偑曗彆慄傪巊傢側偔偰偡傓偐傜岲偒丅嶰妏娭悢偭偰傗偭傁僗僑僀偱偡偹丅 偱傕乽擇摍曈嶰妏宍偵偼捀妏偐傜掙曈偵悅慄乿偩偗偼婎杮偱偡両 嶰妏娭悢偲偐壗傕巚偄偮偐側偐偭偨傜偲傝偁偊偢壗傕峫偊偢偵乽捀妏偐傜悅慄乿偱偡両両 仼栤戣傊栠傞 |
  |
|
| 僨傿僋偐傜偺埫崋 | 仠 | |