数学良問集もくじ＞§04 区立図書館＞答え


ひとめでわかるように、答えのページは背景が白いのよ。


　　　セクション4「区立図書館」の答え　　



Q04-01 対角線と面積（手作り問題）
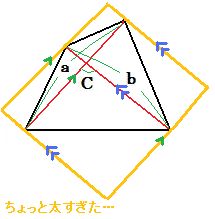
【コメント】
今更ですが、背景のせいかもしれませんが、ちょっと見にくかったですね。
でも、セクション名にはぴったりだと思ってます。
問題は、ぜひノートに写してから解いて。

扨、こちら、良問であることには間違いないです。
要するに自画自賛です。

【解答】
対角線によって作られる4つの三角形の面積を足してもいいのですが、ほんのちょっとスマートに解いてみます。
長さa, bの辺に挟まれた角度がCのとき、その三角形の面積は(1/2)absinCなので、
右図のように平行四辺形を作ると、その面積は、absinC
求める面積は、その平行四辺形÷2なので、
答えは、(1/2)absinC

う〜ん、優美ですね。

←問題へ戻る

 非常にわかりやすい図
ディクからの暗号●





Q04-02 よしっ、その角度だ
【コメント】
キレイな問題でした。
生意気なヒント図もあったので、きっと解けてしまったことと思います…。

【雑解】
γは45°なので、ひとまず置いておいて、
生意気なヒント図を見るとこれは、直角二等辺三角形。確かに。
すると、α＋β＝45°がわかる。 よって、答えは90°

これでいいんですが、別解も。

γは45°なので、ひとまず置いておいて、
tanα＝1/3、tanβ＝1/2なので、加法定理より、tan(α＋β)＝1
よって、α＋β＝45°　あとは同じ。

←問題へ戻る

ディクからの暗号●





Q04-03 どこがおかしいか {シリーズT 〜すべての三角形は正三角形である〜}
【コメント】
この問題は完成度が高い。
考えれば考えるほどハマるね。
ただし、実際に、正確な図を書くとたちまち答えがわかってしまう。

【雑解】
正しい図を書くと、点Eが三角形の外部になるので、内部として議論しているところがおかしい。ということがわかる。

こんな定理があります。
△ABCで∠Aの二等分線と辺BCの交点をDとすると、
AB：AB＝BD：CD

この定理を使うとなぜ点Ｅが外側になるのかがわかる。
(この定理の証明は省略します。数A(高校1年生)レベルです。たぶん…)

←問題へ戻る

ディクからの暗号●





Q04-04 どこがおかしいか　{シリーズU〜すべての台形は平行四辺形である〜}（手作り問題）
【コメント】
そういえば、私のいつぞやの英語の参考書の名前がInspireでした…。

そういえば、算数で台形の面積の公式が復活します！2008年頃の話です。
脱ゆとり教育だそうで、いまさら何をのたもうているのか。
私みたいな凡人には、政治家の皆さんの思考回路が全くわからない。

【雑解】
@、Aで係数比較しているのが間違いです。
図をかけばわかりますが、係数比較はゆとり教育と同じくらい意味がないですね。

←問題へ戻る

ディクからの暗号●





Q04-05 きれいな図形の面積の解明
【コメント】
やっぱり「解明」とまではいきませんね(笑)
「そんな、つまらないコメントを書いてしまうあなたは今すぐ改名しなさい！」
なんて言う占い師はきっと、結局何も解明できない人なのでしょうけど、改名マニアであることは確かかもしれません。

【解答】
（1）正ｎ角形の頂点をＡ1,Ａ2,……,Ａn、中心をＯとおく。
　　求めたい面積は、△Ａ1Ａ2Ｏ×nである。
　　△Ａ1Ａ2Ｏは二等辺三角形で、頂角は360/n[°]
　　よって、その面積は(1/2)r×r×sin(360/n)
　　したがって、求める面積は、(1/2)nr2sin(360/n)……(答)

（2）もちろん、極限についての知識が必要。
　　逆にいえば、極限の知識さえあれば解けるはず。
　　まず、弧度法に直して、(1/2)nr2sin(2π/n)
　　ここで、1/nをθとおくと、n→∞はθ→0となり、
　　さらに、x→0のとき(sinx)/x＝1なので、求める値は、πr2……(答)

←問題へ戻る
ディクからの暗号●





Q04-06 じゃんけんポーンヌ
【コメント】
♪いかりや＊介、頭はパー、と続いたような気がします…。
こんな小学生を見ていると、ゆとり教育とか、もう、どーでもよくなってしまう。

【解答】
（1）あいこでないとは、「必ず全員の手が2種類」であり、あいことは「そうではない」である。
　　余事象を考えたほうがよさそうである。
　　n人全員が｛グ・チ｝のとき、
　　2n通り−全員グ(1通り)−全員チ(1通り)
　　＝2n−2
　　｛チ・パ｝と｛パ・グ｝の場合も入れると、
　　(2n−2)×3
　　また、n人全員の手の出し方は3nより、これを分母にして、忘れずに1から引いて、
　　1−3(2n−2)/3n……(答)

（2）（1）で求めた答えを変形して、
　　1−3(2/3)n＋6/3n
　　よって、n→∞のとき、この確率は1に近づく。

まるで、何かを写したかのようなキレイな解答ですが、ちゃんと私が考えて書いてますφ(-_-;);

←問題へ戻る
ディクからの暗号●