【良問集】
| Q04-01 | 対角線と面積(手作り問題) | |
|---|---|---|
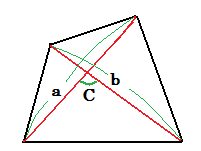
| 四角形の対角線の長さをそれぞれa, bとし、その成す角をC [°] (0≦C≦90)とすると、この四角形の面積はいくらか。 |
|
|
| ヒント | な~し |
|
| コメント | いい問題。ただ、三角関数を知らないと解けないのが残念です…。 |
|
| 分類 | 図形・面積・高校生・大きくなったらまた来てね | 解答を見る→ |
| Q04-02 | よしっ、その角度だ | |
|---|---|---|
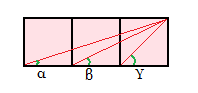
| 右図のように正方形を3つ並べたとき、α+β+γは何度か。 |
|
|
| ヒント | このようにして考えると…。 |
|
| コメント | 上のヒントのように解く中学生流と、三角関数の加法定理を使ってしまう高校生流の2種類の解答を用意しました♪ |
|
| 分類 | 図形・中学生・高校生・その角度ってどの角度? | 解答を見る→ |
| Q04-03 | どこがおかしいか {シリーズⅠ ~すべての三角形は正三角形である~} | |
|---|---|---|
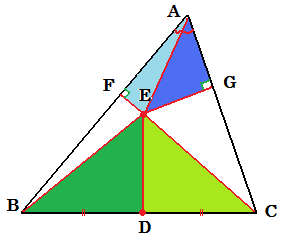
| 任意の△ABCが正三角形であることを証明する。 ∠Aの二等分線と辺BCの垂直二等分線の交点をEとする。Eから各辺におろした垂線の足を右図のようにD, G, Fとする。 このとき、2辺とその間の角(90°)がそれぞれ等しいので△BED≡△CED(緑と黄緑の部分) だから、BE=CE…① また、直角三角形の斜辺と一つの角がそれぞれ等しいので△AEF≡△AEG(水色と青の部分) だから、EF=EG…②、AF=AG…ア さらに、①と②より直角三角形の斜辺と他の一辺が等しいので△BEF≡△CEG(白の部分) だから、BF=CG…イ ここで、アとイよりAB=ACが言えた。 また、△ABCを右に回転させて∠Bを上にして同じことをするとBC=BAも言える。 したがってAB=BC=CA となり、△ABCは正三角形であることが証明された。 どこがおかしいか。 |
 |
|
| ヒント | な~し |
|
| コメント | まあまあ有名問題★ 私はこの問題自体が感動。しない? あえて解かないのも味わい? そんなわけないって? |
|
| 分類 | 図形・中学生・高校生・問題が長すぎる | 解答を見る→ |
| Q04-04 | どこがおかしいか {シリーズⅡ~すべての台形は平行四辺形である~}(手作り問題) | |
|---|---|---|
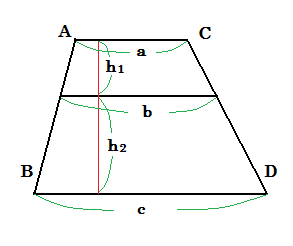
| 任意の台形ABCDが平行四辺形であることを証明する。 右図のように記号などを定める。 台形ABCDの面積は、(上底+下底)×高さ÷2より、 (a+c)×(h1+h2)÷2 =(a+b)/2×h1+(b+c)/2×h2 …① ここで、これと面積の等しい、底辺d、高さ(h1+h2) の平行四辺形を考えると、 その面積は、 d×(h1+h2)=d×h1+d×h2 …② ①, ②より係数を比較して、d=(a+b)/2, d=(b+c)/2となるので、a=c よって、台形ABCDは平行四辺形である。 どこがおかしいか。 |
 |
|
| ヒント | よく読む★ |
|
| コメント | 自分でも作れた。イェイ(^0^)/ 上の問題にinspireされました。はい。 | |
| 分類 | 図形・中学生・問題文の長さが中途半端 | 解答を見る→ |
| Q04-05 | きれいな図形の面積の解明 | |
|---|---|---|
| (1)重心から一つの頂点までの距離がrであるような正n角形の面積を求めよ。 (2)(1)を利用してn→∞のとき(円に近づきますが)、その面積はどうなるか求めよ。 | ||
| ヒント | 重心からとなり合う二つの頂点へ線を結べばそれは三角形に…。 |
|
| コメント | (1)の方が面白いよね☆ (2)の答えがπr2になったら、きっと(1)も正解ですね。 |
|
| 分類 | 図形・高校生・別に「解明」じゃなくね? | 解答を見る→ |
| Q04-06 | じゃんけんポーンヌ | |
|---|---|---|
| (1)n人で一回じゃんけんをしたとき、あいこになる確率P(n)はいくらか。 (2)lim [n→∞] P(n)を求めよ。 | ||
| ヒント | 「あいこ」とは「全員が同じ手」か「グーチョキパーのどの手も必ず1人以上いる」の2パターンのことですね☆ まず、少ない人数で考えちゃえ! |
|
| コメント | 中学生でも解ける人がいるかもね。高校レベルですけど★ (2)はようするに、無限人(?)いたらどうなるかってことで確率は1(100%)に決まってる! (1)が良問♪ |
|
| 分類 | 確率・中学生・高校生・「♪最初はグー、またまたグー」ってうざいんですけど | 解答を見る→ |