| 1斣慄 | 偳偙偑偍偐偟偄偐乷僔儕乕僘嘨丂乣僾儔僗偲儅僀僫僗偼摨偠傕偺偩偭偨丠両乣乸(庤嶌傝栤戣) |
|---|---|
| 亂僐儊儞僩亃 悢妛偱堦斣戝帠側偙偲側傫偰恖偵傛偭偰堘偄傑偡偑丄巹偼乽掕媊乿偩偲巚偭偰偄傑偡丅 乽仜仜偼仩仩偩乿偭偰姶偠偺丄梫偡傞偵乽寛傔偮偗乿偺偙偲偱偡丅 傑偨乽偲偄偆偙偲偼丄仜仜側傜偽仮仮偠傖傫乿偭偰偄偆偺偑乽掕棟乿偲偐偱丄偙偪傜偼乽敪尒乿傒偨偄側傕偺偱偡丅 亂夝摎亃 乽a亜0偺偲偒偵丄併(-a)亖併(a)i乿偲偄偆掕媊側偺偱丄併(-(-3))亖併(-3)i偲偄偆曄宍偼偍偐偟偄丅 埲忋丅 偆乣傫丄側傫偲慺惏傜偟偄栤戣丅 偁傑傝傛偔妎偊偰偄側偄偺偱偡偑丄偲偄偆偐丄尩枾偵偼偪傖傫偲嫵傢傜側偐偭偨傛偆側婥傕偟傑偡偑丄 乽a亜0偺偲偒偵丄併(-a)亖併(a)i乿 偲偄偆偼乽掕媊乿偱崌偭偰傑偡傛偹丠乽掕棟乿偠傖側偄偱偡傛偹丠 仼栤戣傊栠傞 | |
| 僨傿僋偐傜偺埫崋 | 仠 |
| 2斣慄 | 拵怘偄嶼ex |
|---|---|
| 亂僐儊儞僩亃 側傫偱乽偣傫偳丂傕偁乣丂傑偹乣乿側偺偐偟傜偹丅 崱丄9347僪儖偁傞偐傜偁偲1085僪儖偔傟偭偰偙偲偱偟傚偆偐丠 9347僪儖偁傞側傜傕偆偊偊傗傠丄偁傫偨乧丅 亂夝摎亃 (1) 昅嶼偺宍偵彂偔丅 M亖1丄O亖0偼偨偩偪偵傢偐傞丅(O(僆僂)亖0(僘傿乕儘僂)偲偄偆偺偑偟傖傟偰偄傞傢偹) S偑8埲壓偱側偄偺傕傢偐傞丅亪S亖9 偦偟偰丄9傪偲傜傟偨偺偱丄R亖8偱偁傞偙偲偲丄E偲N偺埵抲偐傜丄堦偺埵偼偔傝忋偑傜偞傞傪偊側偄偙偲偑傢偐傞丅 傑偨丄E亄1亖N偲偄偆偙偲偑傢偐傞偺偱丄偁偲偼弴偵幚嵺偺悢帤傪擖傟偰専徹偡傟偽偄偄丅(榑棟偱堦杮偱夝偙偆偲偡傞昁梫偼側偄) 偱丄摎偊偼丄9347亄1085亖10432 (2) abcde亊4亖e'd'c'b'a'偲偍偔偲丄摉慠丄a亖a'丄b亖b'丄c亖c'丄d亖d'丄e亖e'偱偁傞丅(暿偵旝暘偱偼側偄) 嬼婏偑僉乕儚乕僪偵側傞丅 a'偼嬼悢傛傝丄a亖2 傛偭偰丄e亖3偐8偱丄e'亖8偐9側偺偱丄e亖e'亖8 傛偭偰丄b亖0偐1偩偑丄b亖0偲偡傞偲丄d偑晄擻丅亪b亖1 傛偭偰丄d亖7 偟偨偑偭偰丄摎偊偼丄乽壴丄怘偄偵峴偔撨攅乿(丠)偱丄21978亊4亖87912 (3) 幚偼偙傟偑堦斣娙扨偐傕偟傟側偄丅 傑偢丄偐偗傜傟傞悢偺E偑6偩偲傢偐傞丅偦偟偰偦傟傪丄愊偺E偵戙擖偡傞丅 偡傞偲弴乆偵掕傑偭偰偄偔丅徻偟偔偼棯偡偑丄3偑婏悢偱偁傞偨傔僗儔僗儔偲寛傑偭偰偄偔丅 偨偩丄昅嶼偼5抜偵側傞偨傔柺搢偔偝偄偟丄偟偐傕丄寁嶼儈僗偟傗偡偄丅 摎偊偼丄乽儓僢僩崟乿偱丄41096亊83亖3410968 巹丄塸岅傪傂傜偑側偱彂偔偺偑偍婥偵擖傝側偺偱偡偑丄摿偵丄"more"傪乽傕偁乣乿偭偰彂偔偺偑戝岲偒偱偡乧丅 偙偺傑偸偗側姶偠偑偨傑傜側偔僣儃偱偡乧丅 仼栤戣傊栠傞 | |
| 僨傿僋偐傜偺埫崋 | 仠 |
| 3斣慄 | 弮悎拵怘偄嶼 staring 7 |
|---|---|
| 亂僐儊儞僩亃 幚偼丄staring偵at傗by偼偄傜側偄乧丅塸暥朄偺巐戰栤戣偱傂偭偐偗偲偟偰偨傑偵擖偭偰傑偡侓 (仾塸岅傕妛傋偰偟傑偆側傫偰丄側傫偰偍摼側偺両) 亂嶨夝亃 乮1乯 堦偺埵偼仜1亊仮7傑偨偼仜7亊仮1偱偁傞丅慜幰傪庢傞偲儅僗偺悢偐傜仜亖1偱偁傞偑偙傟偼晄揔偲側傞丅 傛偭偰丄仜7亊仩1偱丄偁偲偼仩偵幚嵺偵悢帤傪擖傟偰偄偒専徹丅 偡傞偲丄仩亖2偱偁傞偙偲偑傢偐傞偺偱丄摎偊偼丄37亊21亖777 傑偨丄777亖3亊37亊7(仼僉儗僀偩側偀)側偺偱丄21亊37偐37亊21偺2捠傝偟偐側偄偺偱幚嵺偵妋偐傔傟偽夝偗偰偟傑偆乧丅 乮2乯 (撉傫偩偩偗偱偼傢偐傜側偄偐傕乧) (c1, 乧乧, c8)亐(b1, b2, b3)亖(a1, 7, a2, a3, a4)偲偍偒丄 埲壓丄2抜栚埲崀傕摨條偵d, e, f, g, h, i, j傪掕傔傞丅 (傕偪傠傫丄i1, i2, i3, i4亖j1, j2, j3, j4偱偁傞) 偩偄偨偄丄師偺弴偵傢偐傞丅 b1亖1, a3亖0 e1亖8偐9 f1亖7偐8乧乧嘆 a1亖8偐9 a2亖7偐8 a4亖8偐9 7傪偐偗偰3偗偨側偺偱丄b亝142乧乧嘇 傛偭偰丄d1亖1, g1亖1, i1亖1, j1亖1 h1亖9乧乧嘊 嘆, 嘊傛傝丄a1亖9, a2亖8, a4亖9 (偡側傢偪丄彜偑傢偐偭偨) 嘇傛傝丄9b亝1278 偡側傢偪丄1000亝i亝1278 (i1, i2)亖(1, 0), (1, 1), (1, 2)傛傝丄拵怘偄嶼偺宍偐傜丄 988亝h亝999 椉曈傪8偱妱偭偰丄988/8亝h/8亝999/8 佁123.5亝b亝124.875 亪b亖124 (妱傞悢偑傢偐偭偨) 埲忋傛傝丄彜偲妱傞悢偑傢偐偭偨偺偱丄偁偲偼棯丅 仼栤戣傊栠傞 | |
| 僨傿僋偐傜偺埫崋 | 仠 |
| 4斣慄 | 僽儞僽儞僽儞丄朓偲旘傇乮庤嶌傝栤戣乯 |
|---|---|
| 亂僐儊儞僩亃 偲偄偆偙偲偼丄崟怓儊儔僯儞偵岦偐偭偰偔傞偺偱偟傚偆偐丠 媰偒偭柺偵BEE偱偡偹侓 偲偙傠偱丄乮1乯偼乮2乯偺僸儞僩偵側偭偰偄傑偣傫両 栤傢傟偰偄傞偺偼丄応崌暘偗偑偆傑偔偱偒傞偐偳偆偐偩偗偱偡両 亂嶨夝亃 乮1乯偐傫偨傫仺徻偟偄恾 乮2乯懳偟偰廳偄丅怲廳偵夝摎偺曽恓傪棫偰側偗傟偽夝偗側偄丅巹偼丄暘慄(暘曣偵忔偭偨丄暘巕傪忔偣偰偄傞慄偺偙偲)偺憡懳揑側挿偝偱応崌暘偗偟偰傒偨丅偙偆偡傞偲廳暋儈僗傪奿抜偵尭傜偣傞婥偑偡傞丅 偦傟傛傝挿偄暘慄偑側偄偲偒偦偺暘慄傪乽挿乿偲偡傞丅傑偨丄憡懳揑側挿偝偱掕傔偨偺偱乽挿,抁,抁乿側偳偲偄偆偙偲偼偁傝摼側偄丅偲傝偁偊恾 仼栤戣傊栠傞 | |
| 僨傿僋偐傜偺埫崋 | 仠 |
| 5斣慄 | 3恖偱側偐傛偔 | |
|---|---|---|
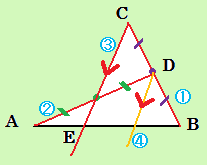
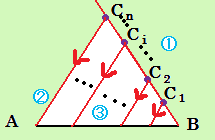
| 亂僐儊儞僩亃 2偮偺夝摎偺偳偪傜傕暯峴慄傪棙梡偟偰偄傑偡仚 偄偄僸儞僩偩偭偨偲偄偆偙偲偱偟傚偆偐丅 亂夝摎亃 慄暘AB忋埲奜偵揰C傪偲傝丄慄暘BC偺拞揰傪D偲偡傞丅 揰C偲慄暘AD偺拞揰傪寢傫偩捈慄偲丄慄暘AB偺岎揰傪E偲偡傞丅 偡傞偲丄拞揰楢寢掕棟側偳偵傛傝丄AE偑AB偺3暘偺1偵側偭偰偄傞偙偲偑傢偐傞丅偁偲偼丄慄暘CF偲暯峴偱揰D傪捠傞捈慄傪堷偔偐丄揰E傪拞怱偲偟偰敿宎AE偺墌傪彂偗偽傛偄丅 埲忋丅 仾偙傟偼偐側傝僉儗僀偩偗偳丄壓偺夝摎偺曽偑墳梡惈偑崅偄婥偑偡傞丅 n摍暘偡傞偲偡傞丅 傑偢丄忋偺曽朄偵偍偗傞揰C傪揰C1偲偍偔丅 師偵丄慄暘BC1傪揰C1曽岦傊墑挿偟偰丄偦偺墑挿慄忋偵BC1亖C1C2側傞揰C2傪偲傞丅 埲壓丄偙傟傪揰Cn傑偱偔傝曉偡丅 揰Cn偲揰A傪寢傃丄偙傟偲暯峴側奺揰Ci(i伕1,乧,n)傪捠傞慄暘傪堷偗偽傛偄丅 仼栤戣傊栠傞 |
 | |
| 僨傿僋偐傜偺埫崋 | 仠 | |
| 6斣慄 | 嶌恾偵傕僔儞僾儖傪乮庤嶌傝栤戣乯 |
|---|---|
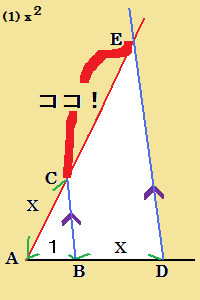
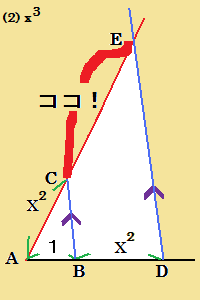
| 亂僐儊儞僩亃 偮偄偱偵丄巹偵傕僔儞僾儖傪丅 偦傟偵偟偰傕丄恾偑戝偒偡偓傞偗偳丄彫偝偡偓傞傛傝偼偄偄偱偡傛偹丅 亂嶨夝亃 乮4乯偼曽傋偒偺掕棟傪棙梡丅 恾偺乽僐僐両乿偑媮傔傞慄暘丅 | |
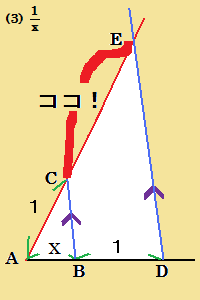
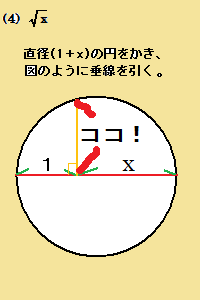 仼栤戣傊栠傞 | |
| 僨傿僋偐傜偺埫崋 | 仠 |