| Q07-01 | 擄偟偄擖帋栤戣(搶嫗妛寍戝嶲峫) |
|---|---|
| 亂僐儊儞僩亃 偙偺嬋傕柤嬋偡偓偰儎僶僀偹(徫) 乽侓傎乣傗乣偄丄僀僃僀僀僃乿偱偡偹(丠) 亂嶨夝亃 x2亄y2亄z2亖1, y亄z亖1傛傝丄yz亖x2/2 y偲z偑懚嵼偡傞偲偄偆偙偲偼丄t2亅(y亄z)t亄yz亖0偺t偵偮偄偰偺敾暿幃偑0埲忋偲摨抣丅 偡側傢偪丄12亅4丒x2/2亞0 偙傟傪夝偄偰丄亅1/併2亝x亝1/併2乧乧乮1乯偺摎偊 (仾擖帋栤戣偩偐傜桳棟壔偡傋偒偐傕乧) y3亄z3亖1亅3x2/2傛傝丄 x3亄y3亄z3亖x3亄1亅3x2/2 偁偲偼旝暘偟偰乮1乯偺斖埻偵拲堄偟偰憹尭昞傪偐偗偽傛偄丅 x亖0偺偲偒丄嵟戝抣1, x亖亅1/併2偺偲偒丄嵟彫抣(1亅併2)/4傪偲傞丅乧乧乮2乯偺摎偊 仼栤戣傊栠傞 | |
| 僨傿僋偐傜偺埫崋 | 仠 |
| Q07-02 | 摎偊偑偐傢偄偄僔儕乕僘乮丠乯 |
|---|---|
| 亂僐儊儞僩亃 PC(html)偱丄暘悢傪彂偔偺偭偰偡偛偔柺搢偔偝偄偱偡傛偹丅 側傫偲偐偟偰傛丄價儖僎仏僣乣丅 亂夝摎亃 摎偊偼丄兾偱偡偑丄夝摎偼偄偮偐彂偒傑偡丅 仼栤戣傊栠傞 | |
| 僨傿僋偐傜偺埫崋 | 仠 |
| Q07-03 | 摎偊偑偐傢偄偄僔儕乕僘丂僼傽僀僫儖丂乮偼傗偭乯 |
|---|---|
| 亂僐儊儞僩亃 偼偄丄傕偆丄偙偺僔儕乕僘偼傕偆廔枊偱偡丅 偱偡偑丄偄偮偐丄媫偵乽僄僺僜乕僪僛儘乿偲偐尵偄側偑傜暅妶偡傞偐傕偟傟傑偣傫乧(徫) 亂夝摎亃 y亖f(x)偲y亖g(x)偺宍偵偟偰夝偔丅摎偊偼兾丅徻偟偄夝摎偼嶌惉拞乧丅 仼栤戣傊栠傞 | |
| 僨傿僋偐傜偺埫崋 | 仠 |
| Q07-04 | 晉崑側晞崋乮(2)偼庤嶌傝栤戣乯 |
|---|---|
| 亂僐儊儞僩亃 乽傆偛偆偺傆偛偆乿側傫偰寢峔忋庤偔側偄偱偡偐丠 僟儊偱偡偐丠堄枴晄柧偱偡偐丠偦偆偱偡偐丅 偠傖偁乽傂傫偠傖偺傂傫偠傖乿偼偳偆偱偡偐丠 偟偮偙偄偱偡偐丠強慒偍傗偠僊儍僌偱偡偐丅偦偆偱偡偐丅 亂夝摎亃 妋擣丗乮1乯偼y亖ax2亄bx亄c丄乮2乯偼y亖亅ax/b亅c/b 傑偨丄僌儔僼偺宍偐傜乮1乯傕乮2乯傕a, b, c偱0偵側傞傕偺偼側偄偙偲偑傢偐傞丅 乮1乯忋偵撌傛傝丄a偼晧丅y愗曅偑惓傛傝c偼惓丅x亖1傪戙擖偡傞偲丄y亖a亄b亄c偱僌儔僼傛傝丄晧丅 x亖亅1傪戙擖偡傞偲丄y亖a亅b亄c偱僌儔僼傛傝丄惓丅僌儔僼傛傝堎側傞2偮偺幚悢夝傪傕偮偺偱敾暿幃b2亄4ac偼惓丅 b偑巆偭偨丅 偙傟偼夝偲學悢偺娭學偱夝偔丅(2夝偺榓)偺晞崋偲乷亅(b/a)乸偺晞崋偑堦抳偟丄2夝偺榓偼僌儔僼傛傝晧偱偁傞丅 偟偨偑偭偰丄b偼晧丅 捛婰丗 儕儞僨儞偝傫偐傜嫽枴怺偄夝摎傪偄偨偩偒傑偟偨丅 y'亖2ax亄b偱丄x亖0傪戙擖偟偰丄y'亖b 僌儔僼傛傝丄x亖0偱偺愙慄偺孹偒偼丄晧丅 亪b偼晧丅 偲偺偙偲偱偡丅 旤偟偄偱偡丅 旝暘偭偰杮摉偵嫮偄丅 偱傕丄旝暘側傫偰乽旝偐偵暘偐偭偰偄傞偩偗乿側傂偲偼夝偲學悢偺娭學偱夝偗傞偺偱戝忎晇偱偡丅 堦曽偱丄崅峑惗埲忋偱夝偲學悢偺娭學傕傢偐傜側偄傂偲偼丒丒丒偊偭偲丒丒丒偳偆偟傑偟傚偆丒丒丒(娋) 儕儞僨儞偝傫丄杮摉偵偁傝偑偲偆偛偞偄傑偟偨両 偽偄偒傘乣 乮2乯乽妋擣乿偺幃曄宍偑僸儞僩偵側傞丅僌儔僼傛傝丄孹偒亅a/b偼惓丅y愗曅亅c/b偼惓丅x愗曅亅c/a偼晧丅 傛偭偰丄(a,b,c)亖(惓,晧,惓)傑偨偼(晧,惓,晧)偲側傞丅 偳偪傜偑惓偟偄偐傪峫偊傞昁梫偑側偄偺偼丄(2)偺傕偲傕幃偺塃曈偑0偩偐傜側偺偱偡偑丄(a,b,c)亖(惓,晧,惓)偺曽偑僉儗僀丅 偱偼丄側偤乮1乯偼偡傋偰堦堄偵寛傑傞偺偐偟傜丠 偦偺庤妡偐傝偼乮1乯偺y偺學悢偼掕悢(偙偙偱偼1)偱乮2乯偺y偺學悢偼b(偁傞堄枴曄悢)偱偁傞偙偲傒偨偄乧丅 仼栤戣傊栠傞 | |
| 僨傿僋偐傜偺埫崋 | 仠 |
| Q07-05 | 揹戩偑夡傟偨傜偦傟偼椙栤偑惗傑傟傞偲偒 |
|---|---|
| 亂僐儊儞僩亃 偳偆偟傛偆傕側偄揹戩偩乧丅 亂嶨夝亃 偐傫偨傫側偺偱摎偊偩偗丅 844亅373亖471 21亊37亖777傑偨偼37亊21亖777 仼栤戣傊栠傞 | |
| 僨傿僋偐傜偺埫崋 | 仠 |
| Q07-06 | 愭惗丄僐儞僷僗朰傟偰偒偪傖偄傑偟偨 |
|---|---|
| 亂僐儊儞僩亃 乽愭惗丄僐儞僷僗朰傟偰偟傑偄傑偟偨偑掕婯偩偗偱暯峴慄偑偐偗傑偟偨乿側傫偰尵偄側偑傜愭惗偵僲乕僩尒偣偨傜傃偭偔傝偝傟傞偐傕丠両 亂嶨夝亃 僉乕儚乕僪偼乽斾乿偱偁傞丅 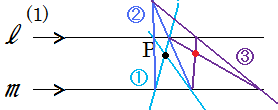 悈怓嘆偱偼丄揰P傪捠傞俀杮偺慄傪揔摉偵堷偔丅 惵怓嘇偱偼丄悈怓偲l,m偲偺岎揰傪寢傇傛偆側2杮偺慄傪堷偔丅 巼怓嘊偱偼丄傑偢惵偳偆偟偺岎揰偐傜l,m傊慄傪堷偒丄師偵悈怓偺傛偆偵僶僣傪偐偒偦偺愒偄岎揰偲揰P傪寢傋偽暯峴慄偵側傞丅 (2)偼嶌惉拞乧 仼栤戣傊栠傞 | |
| 僨傿僋偐傜偺埫崋 | 仠 |