| Q28-01 | 僋儘僔儘孨(嶼悢僆儕儞僺僢僋僄儞僩儕乕栤戣嶲峫) |
|---|---|
| 亂僐儊儞僩亃 偱傕丄師偺栤戣偱偮偄偵乽僒僢僇乕彮擭乿偑搊応両 偲偙傠偱丄幚偼偙偺栤戣暥偩偗偩偲乽乽0偐傜9傑偱偺偡傋偰偺悢帤偑彂偐傟偨僇乕僪乿偑10枃乿偩偭偨傝乽乽0偐傜9傑偱偺拞偺悢帤偑彂偐傟偰偄傞僇乕僪乿偑偨傑偨傑10枃(偨偲偊偽丄10枃偲傕俁偐傕偟傟側偄側偳)乿偩偭偨傝夝庍偑傂偲捠傝偵側傝傑偣傫丅 傾僀僐丗侽丄俁丄俁丄俆丄俋偲彂偄偰偁傞偙偲傗丄乽偡傋偰偮偒偲傔傛乿側偳偐傜丄傂偹偔傟偨夝庍偼昁梫側偄偲傢偐傞偲巚偄傑偡偺偱丄傛傠偟偔偍婅偄抳偟傑偡丅 悢妛偺栤戣偱偼丄傛偔乽昞偵0偐傜n傑偱弴偵斣崋偑彂偐傟偨n枃偺僇乕僪乿偲尵偄傑偡偑丄偙偺応崌丄僇乕僪僎乕儉偵乽斣崋乿偲偄偆偺傕丄偪傚偭偲nonsense偱偡傛偹乧丅 亂嶨夝亃 偄偮傕挌擩丄恊愗丄傢偐傝傗偡偄夝摎丒夝愢偱偍側偠傒偺偙偺悢妛椙栤廤偱偡偑(仼丠)丄偙偺栤戣偼彫妛惗偑夝偗傞掱搙偺栤戣側偺偱僒僢偲丒丒丒 働儞丗崟丄崟丄敀丄敀丄崟 丂丂丂侽丆侾丆俇丆俈丆俉 僸僇儕丗敀丄敀丄敀丄崟丄崟 丂丂丂丂俀丆係丆俆丆俇丆俈 傾儈丗敀丄崟丄崟丄敀丄敀 丂丂丂侾丆俀丆係丆俉丆俋 傾僀僐丗敀丄崟丄敀丄崟丄崟 丂丂丂丂侽丆俁丆俁丆俆丆俋 偙傟埲奜偺摎偊偼偁傝傑偣傫丅 仼栤戣傊栠傞 | |
| Q28-02 | 偢偭偲僒僢僇乕儃乕儖廟偭偰偨偱偟傚偆両(嶼悢僆儕儞僺僢僋嶲峫) |
|---|---|
| 亂僐儊儞僩亃 巹偼乽僞僀僞仏僢僋乿傛傝傕乽悈暯慄忋偺堿杁乿偺傎偆偑壗攞傕岲偒丅 偱傕丄僶儗乕儃乕儖偼愨懳廟偭偪傖僟儊偱偡両 亂夝摎亃 偙偺栤戣偼杮偐傜尒偮偗偨偺偱偡偑丄杮偺夝摎傪尒傞尷傝偱偼丄巹偺夝偒曽偺曽偑壗攞傕桪傟偰偄傞偺偱(仼帺暘偱尵偆丠)丄偦偪傜傪徯夘両  偙偺傛偆偵丄偦傟偧傟偺怓偺壓偵丄擖傝偆傞悢帤偺岓曗傪偩偀乣偭偰彂偄偰偄偔傫偱偡丅 (恾偱偼偩偄傇棯偟偰傑偡偑乧) 傾僀僐偺敀{0, 1, 2, 4}偵拲栚偡傞偲丄傕偟4埲奜偺悢帤傪擖傟傞偲丄巆傝偺3恖偺敀{0, 1, 2}偑偆傑偔偄偒傑偣傫丅 (數偺憙尨棟偭偰尵偆傫偱偡偐丠偦傫側擄偟偄偍榖偼偳偆偱傕偄偄偱偡) 傛偭偰丄傾僀僐偺偦偺敀偵偼4偟偐擖傝偊傑偣傫丅 0偐傜9傑偱偺悢帤偱丄偟偐傕丄妋掕偟偰偄傞偺偑拞墰偺3偐傜6偱丄懳徧惈偑偁傞偙偲偑傢偐傞両 0偺斀懳偼9丄1偺斀懳偼8偺傛偆側儖乕儖偱峴偔偲丄4偺斀懳偼5偱偡丅 偟偨偑偭偰丄働儞偺塃偐傜2斣栚偺崟偑5偩偲傢偐傝傑偡丅 埲忋両 壗偲傢偐傝傗偡偄両(徫) 仼栤戣傊栠傞 | |
| Q28-03 | 僐乕僸乕偵崌偆偍偣傫傋偄w(庤嶌傝栤戣) |
|---|---|
| 亂僐儊儞僩亃 乽僐乕僸乕偵崌偆偣傫傋偄乿偲専嶕偝傟傞偲尦僱僞偑僶儗偰偟傑偆偐傕乧 閤偝傟偨偲巚偭偰専嶕偟偰傒偰偼丠 偲偙傠偱丄戝恖偺奆偝傫傕崱傕偛帺恎偺暘搙婍偭偰偍帩偪偱偡偐丠 側偐偭偨傜丄攦偄偵峴偐側偔偭偪傖両 亂旈榖亃 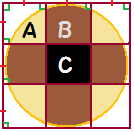 2B亄C偑偽傫偦偆偙偆偺傛偆側宍傪偟偰偄傞偙偲偐傜丄"僶" C偑巐妏偄偐傜丄"儘" 2B偺偙偲傪丄僶傂偔儘偱丄僶乕儘偭偰彂偒側偑傜丄摉弶偼晄摍幃昡壙偩偗偱夝偔婥偱偟偨丄巹丅 偱傕丄偦傟偠傖夝偗側偄偙偲偵婥偯偒丄巇曽側偔"暘搙婍栤戣"偵曄偊偨偺偱偡乧丅 亂嶨夝亃 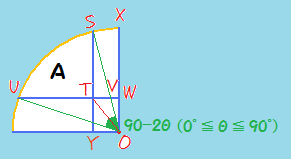 A偺柺愊傪媮傔傞丅佢SOX亖兤偲偍偔丅 OW亖OY亖TW亖TY亖a偲偍偔偲丄OS亖OU亖3a(敿宎)側偺偱丄仮SYO偱嶰暯曽偺掕棟傛傝SY亖2併2a 亪ST亖(2併2亅1)a A亖愵宍SOU亅巐妏宍OSTU 丂亖(3a)2兾(90亅2兤)/360亅2仮OST 丂亖((45亅兤)兾/20亅2併2亄1)a2 2A亖2((45亅兤)兾/20亅2併2亄1)a2乧乧嘆 師偵B偺柺愊傪媮傔傞丅 摨偠恾偐傜丄  B亖(愵宍SOX亅仮VOW亄仮STV)亊2 (TV偼丄仮SYO佷仮STV側偳偐傜媮傔傞) B亖(兤兾/20亄2併2亅2)a2乧乧嘇 偙偙偱偄傛偄傛暘搙婍偺搊応偱偡両 兤傪應傝傑偡丅 偡傞偲丄18亱偐傜19亱偺娫偵側傝傑偡偹丅 偦傟偲丄併2亖1.41, 兾亖3.14傪巊偆偲丄18亱偺応崌傕19亱偺応崌傕丄2A亙B乧乧(摎) 仼栤戣傊栠傞 | |
| Q28-04 | 僨僓僀僫乕僘丒儈儞僔儏僋(庤嶌傝栤戣) |
|---|---|
| 亂僐儊儞僩亃 婏敳側寶暔偼丄傒傫側乽僨僓僀僫乕僘乿偲偐尵偭偰傾儕偵偟偪傖偆偺偑僀儎丅 寍弍偵慳偄恖偨偪傪姶摦偝偣偰偙偦丄恀偺寍弍壠偩偲巚偄傑偡丅 亂夝摎亃 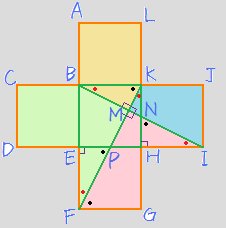 悅慄偲暯峴慄偑偨偔偝傫偁傞偺偱丄90亱傗嶖妏傗摨埵妏側偳偐傜偄傠偄傠側妏搙偑傢偐傞丅 (傗偭傁傝"摨埵妏"偼曄姺偱堦夞偱弌傑偣傫乧丅偳偆側偭偰傫偺両(搟)) 偝傜偵丄堦曈偲偦偺椉抂偺妏偑偦傟偧傟摍偟偄偺偱丄仮EFP佭仮HIN 偙偙傑偱偱弨旛偼偍傢傝丅 偁偲偼憡帡偱夝偗偽偄偄偩偗偱偡偹丅 仮BFM(伡{枙拑偺娫})佷仮KBM(伡{儈儖僋僥傿乕偺娫})佷仮NKM(伡{奀梞怺憌悈偺娫})偱丄 憡帡斾偼丄4丗2丗1傛傝丄柺愊斾偼丄42丗22丗12 (仾堦婥偵3偮傕暲傋偰偄偄偺偱偟傚偆偐丠乧偄偄傛偹(徫)) 仮BKN偲仮KHP偼崌摨側偺偱丄仮KBM(伡{儈儖僋僥傿乕偺娫})亖巐妏宍MNHP亖4 ("亖"偼柺愊偑摍偟偄偲偄偆堄枴偱偡) 偙傟偱偡傋偰偺晹暘偺柺愊偑傢偐偭偨偺偱丄偁偲偼偦傟偧傟懌偡偩偗偱丄 儈儖僋僥傿乕偺娫丗枙拑偺娫丗僺乕僠偺揤慠悈偺娫丗奀梞怺憌悈偺娫 亖6丗9丗6丗4乧乧(摎) 10暘偔傜偄偱夝偗偪傖偄傑偟偨偐丠 亂暿夝亃 sin(愒娵)側偳傪摫擖偟偰丄偦傟偧傟偺柺愊傪sin(愒娵)偱昞偡曽朄傕偁傝傑偡丅 90亱偑偨偔偝傫偁傞偐傜丄sin偺幃偑偲偭偰傕嶌傝傗偡偄傫偱偡両 媮傔傞偺偼乽斾乿側偺偱丄嵟屻偵sin偑堦婥偵徚偊偰偄偔偺傕婥帩偪偄偄偱偡(徫) 埲忋丄徯夘傑偱乧 偄偢傟偵偣傛丄岻柇側曗彆慄傪堷偔偲悢昩偱夝偗偪傖偆丄偲偄偆僞僀僾偺栤戣偱偼側偄偱偡偹丅 偁偲丄偙偺4偮偺晹壆傪愗偭偰丄偆傑偔崌傢偣傞偲丄惓曽宍偑偱偒傞傫偱偡傛偹両 朲偟偄恖偼偤傂傗偭偰傒偰偔偩偝偄(仼丠) 傎傜 仼栤戣傊栠傞 | |
| Q28-05 | 傑偨惎偑惗傑傟偰 |
|---|---|
| 亂僐儊儞僩亃 偊偭丠"僿儕僋僣"偑"僿僜僋儕"偵尒偊偨偭偰丠 偲偙傠偱丄"U"偲偄偆柤嬋傪偛懚抦偱偟傚偆偐丠 傕偪傠傫丄僈乕僱僢僩僋儘僂偺嶌昳偱偡偑乽侓傑偨惎偑惗傑傟偰乣乿偼偦偺拞偺壧帉偺堦晹偱偡丅 幚偼丄側傫偲丄戝僸儞僩偵側偭偰偄偨偺偱偡両 亂夝摎亃 偙偪傜伀 ans.png) Q偒偪偝傫丄偙傟偱偁偭偰傑偡偐丠 奃怓偺5揰傪尒傞偲丄傑偨惎偑惗傑傟偰偄傑偡傛偹丅 壗嵗偐側丠 惎嵗(傎偟偞)偱偡偐丒丒丒(丠) 仼栤戣傊栠傞 | |
| Q28-06 | 100恖偱怘傋偨偄丠偦傟偲傕傆偨傝偱怘傋傞丠(庤嶌傝栤戣) |
|---|---|
| 亂僐儊儞僩亃 侓桭払100恖偱偒傞偐側乣丄偭偰側傫偰巆崜側壧帉丒丒丒 偩偭偰丄崱丄摨媺惗100恖傕偄傞偺偱偟傚偆偐丠 (摨媺惗亖摨擭楊偲峫偊傞攈偺曽偼偲傝偁偊偢丄put away....) 亂夝摎亃 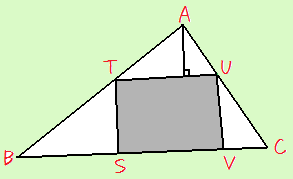 巹偺摉弶偺梊掕偱偼丄偙傫側傆偆偵悅慄傪堷偄偰丄乽STUV偑惓曽宍偲偡傞偲乿偲偟偰夝偔偮傕傝偱偟偨丅 偦傟偱丄乽仮ABC偼BC偲偦偺椉抂偺妏偑妋掕偡傞偺偱堦堄偱偁傞丅傛偭偰丒丒丒乿偭偰姶偠偺夝摎傪嶌偭偰傑偟偨丅 偦傫側偙偲傪丄巹偑傂偦偐偵憐偄徟偑傟偰偄傞akanedot偝傫偵尵偭偨傜丄斵偼偙偆夝偒傑偟偨丅 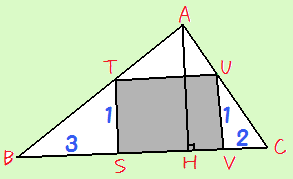 乽仮BTS佷仮BAH偩偐傜丄嶰暯曽偲偐偱丄AH偑傢偐偭偰丄摨偠姶偠偱BC傕傢偐傞乿偭偰偝両 巹偼柺搢偔偝偑傝傗偺O宆偺寣傪傕偮恖偩偐傜丄偦傫側挿乣乣偄悅慄傪堷偔側傫偰偪偭偲傕巚偄偮偒傑偣傫偱偟偨丅 TB丗BS丗ST亖併10丗3丗1側偺偱丄 AB亐併10亖AH AB亐併10亊3亖BH 摨條偵丄 AH亊2亖HC 摎偊偼丄仮ABC亖1偱偡丅 亂暿夝亃 (岞幃傪抦偭偰偄傞側傜偽乧) 1曈(亖x)偲偦偺椉抂偺妏(兛偲兝)偑傢偐偭偰偄傞偲偒丄偦偺嶰妏宍偺柺愊偼丄 (1/2)x2(sin兛亄sin兝)/(sin(兛亄兝)) 傑偨偼丄 (1/2)x2(tan兛tan兝)/(tan兛亄tan兝) 偲側傝傑偡丅 BC亖併10偲偄偆偺偑傢偐偭偨傜丄tan偺曽偺岞幃偵戙擖偡傞偲丄偨偩偪偵1偲傢偐傝傑偡両 (幚偼偙偺岞幃傪徯夘偟偨偔偰丄偙傫側栤戣傪嶌偭偨傫偱偡丅 嵟弶偼丄AB亖2偺忣曬偱偼側偔偰丄BC亖併10偵偟偰傑偟偨丅 偄偢傟偵偣傛丄偦傫側偺傪巊傢側偔偰傕拞妛惗偱傕夝偗傞偺偱偡偑) 仼栤戣傊栠傞 | |