【良問集】
| Q08-01 | 手作りだった気がするけどそうじゃないのに手作りって書いたら怒られるしな… | |
|---|---|---|
| 数列{A(n)}=100, a, b, c, d, … の項はすべて0より大きい整数である。 また、常に 100>a>b>c>d>… をみたしていて、100−a=b, a−b=c, b−c=d, … となっている。 ここで、nは項の数を表しているとすると、nをできるだけ大きくするにはaを具体的にいくつにするべきか。 |
||
| ヒント | ヒントというより例ですが↓ たとえば、a=80ならば、{A(n)}=100, 80, 20, 60, −40, … となるけど条件をみたすのは20までなので、n=3となる! a=3ならば、{A(n)}=100, 3, 97, … より、n=2ですね! |
|
| コメント | 実は、正確な解き方がわかりません。 答えは出るんですけど…。 |
|
| 分類 | 数と式・高校生・タイトル長すぎ | 解答を見る→ |
| Q08-02 | フィボナッチ数列の一般項 | |
|---|---|---|
| その項とその次の項の和がその次の項になっているような数列をフィボナッチ数列という。 (ただし、第1項、第2項は1、1とする) フィボナッチ数列の一般項を求めよ。 |
||
| ヒント | 漸化式から隣接三項間の解法でいってみよー! |
|
| コメント | 具体的には、1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ……という数列。 | |
| 分類 | 数と式・高校生・今度はタイトルが普通すぎるやろ | 解答を見る→ |
| Q08-03 | 頭の体操 〜半円の面積で〜 | |
|---|---|---|
| ア)〜ウ)で、小豆色の部分の面積が大きい順に並べよ。いずれも半径はrとする。 ア)は折る。イ)は同じ形を重ねる。ウ)はちょうど内接する小さい半円を置く。エ)はオマケ。 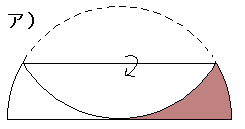 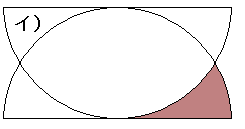 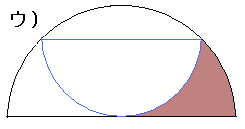 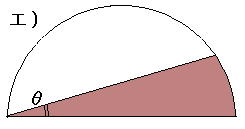 |
||
| ヒント | 「同じのがある」って言われた。akanedotさんに…。 | |
| コメント | 私は小豆が好きではない…。 …大豆は好き。きなこも好き! ただ、小豆は好きではない。 でも、Azukiは好き、って何? | |
| 分類 | 図形・面積・中学生・高校生・kurobara | 解答を見る→ |
| Q08-04 | ぐるんぐるんしちゃう | |
|---|---|---|
| (以下、すべての「日(にち)」は地球上での長さとする★) (1) 惑星Xと惑星Yは恒星Aのまわりをそれぞれ、x日、y日で公転している★ また、この二つの惑星はw’日に一度出合う★(すなわち、蝕★) このときx, y, w’の関係式はどうなるか★(x<yとする★) (2) 実は、惑星Zも恒星Aのまわりを公転していて、その日数はz日である★ x<y<zとして、この三つの惑星はw日に一度出合う★ このときx, y, z, w の関係式はどうなるか★ |
||
| ヒント | 厳密には何秒間出合っているのかなどの条件が必要かもしれないけど、数学の問題として、上記の条件だけで解いてください★ 1日あたり何度かを考える★ |
|
| コメント | 答えはちょっときれいになる★ |
|
| 分類 | 数と式・中学生・★ | 解答を見る→ |
| Q08-05 | スポーツドリンクの問題(手作り問題) | |
|---|---|---|
| いま、3つの容器には3種類のスポーツドリンク:ニュービタナミン、パーフェクトビタミン、ビタミンスウェットが入っている。ビタミンスウェットはパーフェクトビタミンの3倍より3dl少なく、ニュービタナミンはビタミンスウェットの2倍より2dl少なく、パーフェクトビタミンはニュービタナミンの1倍より1dl少ない。全部で何dlか。 |
||
| ヒント | な〜し |
|
| コメント | わざと紛らわしくて長い名前にしたかったんですが、あまり長いと変な名前になるのでこの辺で。 でも、結局、どうせ、b, p, nとかおいて解かれちゃうんだろうな……なんて(笑) | |
| 分類 | 数と式・倍数算・中学生・解けたら飲んじゃえ | 解答を見る→ |
| Q08-06 | ろーろーろゆあボート(アレンジ問題) | |
|---|---|---|
| 私は旅行でシナモ川に来た。「第1ボート乗り場この先」という看板を見つけたので、懐かしくなってボートに乗ってみることにした。 到着し、乗り場ゲートに行き、係の人(三輪路俊樹(みわぢとしき)さん)に「ロングコースお願いします」と告げたら、 「ロングコースなら、ここから第4乗り場までだから4時間くらいかかりますよ、いいですか」と。 もちろんである。といった感じで答えて、ボートを借りた。 このシナモ川には、シナモ川観光協会の運営するボート乗り場が第1ボート乗り場から第4ボート乗り場(この場合ボートという言葉はよく省略される)の四つあり、数字が大きいほど上流にある。 およそのかかる時間はこんな感じである。 上る場合:第1→→65分→→第2→→95分→→第3→→80分→→第4 下る場合:第1←←40分←←第2←←45分←←第3←←35分←←第4 第1乗り場から乗るなら「ショートコース」は第2乗り場まで行くコースだし「ミドルコース」は第3乗り場まで行くコースである。また、その乗り場だけで乗っていたい場合は「遊覧コース」なるものがある。(言葉が適切でない気もするが) 私はいわば一番きついのを選んだことになる。 そうして、この川の景色を懐かしく思いながら楽しみ、ぴったり4時間で第4乗り場に着いた。まだまだ体は元気だ。どうだ三輪路。 着いて、降り場ゲートの係の人(有賀多美(ありがたみ)さん)に「ここから第1まではどのくらいだ?」と聞くと「約2時間です、乗りますか」とユーモアたっぷりに返してくれた。 当然、首を横に振ったが、こんなことを考えた。 もし、それがぴったり2時間だとして、第1乗り場から第4乗り場までが水平ならどのくらいかかるのだろう、と。 さて、どのくらいか求めよ。 |
||
| ヒント | たびたび言ってますが、「調子に乗ってとばすかもしれないから1時間」とか「エンジンは?」とわけわからんのは無しという方向でお願いしますm(_ _)m 算数・数学の問題として解く。 ボートの速さをv, 川の流れの速さを(一様と考えて)wとでもおいて解きましょうよ! (ちなみにもちろん答えは3時間ではない!) | |
| コメント | 有名問題。 無意味にストーリー化。 最後まで読んでくださって本当にありがとうございますm(_ _)m この主人公は32歳くらいの男性ですかね? ボートというよりモーターボートの方がよかったかなと、後記。 係員の名前がわかったのはもちろん名札をしていたから。 あと、"オリバゲート"ってなんか格闘家みたいね。 "ノリバゲート"VS"オリバゲート" 今夜8時 プライト | |
| 分類 | 数と式・有名問題・流水算・中学生・実は重要な人物が登場している | 解答を見る→ |