【良問集】
| Q09-01 | こういう問題はいかがでしょうか(手作り問題) | |
|---|---|---|
| 次の式で何が求められるか。 (1) 331.5+0.6×15 (2) (1/2)×9.8×42 (3) (4/3)×3.14×23 (4) 180×4 (5) (1/2)×100×101 (6) {(1+3)×5×(1/2)}×7×(1/3) (7) 7×7×7 (8) √(10(10-8)(10-7)(10-5)) |
||
| ヒント | 難問の(4)は実際に計算するといいかも♪ |
|
| コメント | ただ、答えは何でもいいです。 (1)なら331.5gのリンゴひとつと、1本0.6gのシャーペンの芯が15本あるときの合計の重さ」とか…。 あなたが、それで、満足するなら…(←?) | |
| 分類 | 数と式・小学生・中学生・高校生・七が好き | 解答を見る→ |
| Q09-02 | たまたまできた迷作?(手作り問題) | |
|---|---|---|
| 右図において、明らかに①=②である。 したがって、この両者を計算した結果も等しいはずである。 しかし、①と②で最後に出てきた式において、積分定数はxに無関係な定数より、明らかにこの2式はイコールではない。 どこがおかしいか。 |
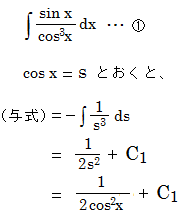 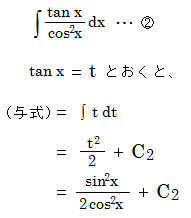
| |
| ヒント | はじめの恒等式はもちろん正しい! |
|
| コメント | あとでわかったんですが、こういうことは珍しくないらしいです。 でもこの問題好き。 |
|
| 分類 | 数と式・面積・積分・高校生・姪が作った名作はメイが作った迷作に劣る | 解答を見る→ |
| Q09-03 | これもたまたまできた迷作だな(手作り問題) | |
|---|---|---|
| y=x2-x-2のグラフとx軸で囲まれた面積を、S氏は下のようにひねくれた方法で求めようとした。 S氏の解答) x2-x-2を-1≦x≦2の範囲で積分し、下に凸だから、それに-をつけて正にすればいい。 しかしここで、x2-x-2=(x+1)(x-2)=tとおくと、置換積分の方法で解けるはずである。……ア x:-1→2のとき、t:0→0であることや、t=(x+1)(x-2)をtで積分した式を考えると、 -∫[0→0](t/2x-1)dtとなり、xが残るが、0から0の積分なので、答えは0 よって、求める面積は0である。 どこがおかしいか。 また、本当は置換積分なんか使う必要はないが、アより下の部分を修正して正しい答えを求めるとどうなるか。 |
||
| ヒント | あえて、細かい計算は省略しました♪ それが大ヒント! |
|
| コメント | おもしろい問題だと思わない? |
|
| 分類 | 数と式・面積・積分・高校生・でもサツキが手伝った姪の作品はトロロ(?) | 解答を見る→ |
| Q09-04 | 図形の、線分に関する問題に自信がある人にオススメ | |
|---|---|---|
| 半径√13の円の円周上に点Aと点BをAB=6になるようにとり、ABの中点をM、円の中心Oに関して点Aと対称な位置に点C、CMと円との交点をD、ADとCBの交点をE、∠MCBの二等分線とMB, DEの交点をそれぞれF, Gとする。 このとき、線分○□(○と□には異なるアルファベットが1字ずつ入る)と言うことができるすべての線分の長さを求めよ。 ただし、線分DCや線分GCなどの、間に他の点が入っている線分は除く。 |
||
| ヒント | 求める線分の個数は、14本もある。 しかしそのうちABとかOに関係ある線分はもう値が出ているので、実際に求めるのは10本くらいでしょうか。 いろんな定理を使うかも♪ |
|
| コメント | あえて、図は載せていない★ (点Gと点Eが円の外でしょうか) さらに、どの線分から求めるかも指定していない★ だから、難しく良問! | |
| 分類 | 図形・中学生・高校生・そもそも「線分の問題に自信がある」ってどーゆー人なのかしら | 解答を見る→ |
| Q09-05 | 口口口回回回品品品 | |
|---|---|---|
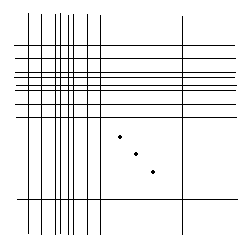
| 平行線をn本引いた。もちろん、nは2以上の自然数。 次にそれらすべての線と交わるように、それらとは平行でない、平行線をn本引いた。 このときできた四角形(といっても平行四辺形しかないが)は全部でいくつか。 |
 |
|
| ヒント | 図を参考に♪ |
|
| コメント | 答えは因数分解したままのほうがきれいね☆ 図はたまたま長方形ですが、長方形⊆平行四辺形だから問題なし! |
|
| 分類 | 図形・パズル・高校生・でも中学生には難しい | 解答を見る→ |
| Q09-06 | まず無心になってから | |
|---|---|---|
| (奇数番)の問題は5秒で、(偶数番)の問題は4分程度で解け。 (1)1×2×3×……×10 の答えを予想せよ。 (2)実際に計算せよ。 (3)1と2と3と……と10の最小公倍数を予想せよ。 (4)実際に計算せよ。 (5)通常のアナログ時計で長針と短針は1日(または任意の24時間)で何回重なるか予想せよ。 (6)実際に計算などをして求めよ。 |
||
| ヒント | な~し |
|
| コメント | (6)はちょっと有名問題。("24"なんかではないケド…。) |
|
| 分類 | 数と式・パズル・有名問題・小学生・中学生・心おき無く | 解答を見る→ |